Mécanique quantique: ses 7 merveilles

La mécanique quantique, c’est cette branche de la physique qui décrit la manière dont se comportent les objets microscopiques : les molécules, les atomes ou les particules.

Développée pendant la première moitié du XXème siècle, la mécanique quantique est un des piliers de la science contemporaine. Et pourtant, il s’agit aussi probablement de la plus étrange théorie jamais imaginée.

En effet, la mécanique quantique regorge de mystères, de surprises et de paradoxes qui nous obligent à revoir la manière dont nous concevons la matière, et même la physique en général.

Cette théorie est d’ailleurs tellement bizarre que l’un de ses plus fameux contributeurs, le physicien Richard Feynman (ci-dessus), disait à son propos:

« Si vous croyez comprendre la mécanique quantique, c’est que vous ne la comprenez pas ».

Nous voici prévenus ! Mais essayons quand même d’y voir plus clair. Aujourd’hui, je vous propose donc un tour d’horizon des 7 merveilles et mystères de la mécanique quantique. Âmes sensibles, vous pouvez rester, je vous promets de ne pas employer de connaissances au delà du lycée !

1. Le principe de superposition

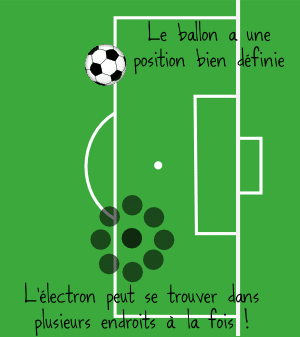
Quand on étudie le mouvement des objets du quotidien, par exemple un ballon de foot, on considère des quantités bien définies : sa vitesse, sa position, sa vitesse de rotation ou son énergie.

On ne sait pas forcément mesurer très exactement ces quantités, mais on sait qu’elles existent et qu’elles ont des valeurs précises. A un instant donné, le ballon de foot est dans un état bien défini. Ça, c’est la mécanique dite « classique », c’est-à-dire celle des objets normaux.

Mais pour les objets microscopiques, tout change ! Contrairement au ballon de foot, une particule microscopique peut être dans un mélange de plusieurs états. Aussi incroyable que cela paraisse, cela veut dire qu’un électron peut par exemple posséder à la fois deux vitesses, ou être à deux endroits différents à la fois. Voire même plus de deux endroits !

Pour désigner le fait qu’en mécanique quantique, les objets peuvent être dans plusieurs états à la fois, on parle du principe de superposition.
Les physiciens ont une notation bizarre pour désigner ça, il décrivent les états avec des sortes de crochets comme celui-ci , et pour superposer des états ils  les additionnent.

Vous avez certainement déjà entendu parler de cette étrange superposition à travers l’exemple du fameux chat de Schrödinger, ce chat « fictif » qui serait à la fois mort et vivant. En utilisant cette notation entre crochets, on pourrait écrire :

|Chat> = | Mort > | Vivant >

Bien sûr, l’exemple du chat n’est pas très réaliste, car je vous l’ai dit cette situation ne peut se produire que pour les objets microscopiques. Et heureusement ! Vous imaginez si le ballon de foot pouvait se trouver à la fois derrière et devant la ligne de but !

Vous allez voir que de cette simple idée de superposition des états découlent toutes les étrangetés de la mécanique quantique.

2. L’indéterminisme de la mesure

Continuons notre comparaison entre la mécanique classique et la mécanique quantique. En mécanique classique on peut mesurer les propriétés des objets, par exemple la vitesse du ballon de foot. On peut bien sûr faire des erreurs de mesure (par exemple mesurer 133 km/h alors que la vraie valeur est 132 km/h pour la frappe de Roberto Carlos). Mais si on améliore la précision de notre instrument, on va se rapprocher de plus en plus de cette vraie valeur.

Mais comment ça se passe en mécanique quantique ? Imaginez un électron qui aille à la fois à 1000km/h et 2000 km/h. Je vous rappelle qu’on va noter cela comme ça :

|électron> = |1000 km/h > |2000 km/h >

Si on mesure la vitesse de cet électron, que va-t-on trouver ? 1000 km/h ? 2000 km/h ? Entre les deux ?

Ce que nous dit la mécanique quantique, c’est qu’on va trouver soit l’un, soit l’autre, mais qu’il n’existe aucun moyen de savoir à l’avance lequel des deux. Le résultat de la mesure est probabiliste. Le pire étant que même si on imagine refaire plusieurs fois l’expérience exactement de la même manière, on ne trouvera pas forcément le même résultat que la fois d’avant. En fait dans la situation que je décris, vous allez trouver 1000 km/h dans 50% des cas, et 2000 km/h dans 50% des autres.

On peut même avoir des variantes de cette situation où l’on mélange des états avec des proportions différentes, comme dans un cocktail. Par exemple on peut écrire le mélange suivant :

(1/4) | 1000 km/h > (3/4) | 2000 km/h >

Ici l’électron est 3 fois plus dans l’état 2000km/h que dans l’état 1000 km/h. Et devinez quoi ? Cela modifie les probabilités lors des mesures. Avec un électron dans cet état, vous mesurerez bien plus souvent 2000 km/h que 1000 km/h (les proportions ne seront pas tout à fait 1/4 et 3/4, mais ça n’est pas important à ce stade).

Ce que je vous décris là est une révolution conceptuelle incroyable en physique. Les physiciens ont longtemps supposé que la nature était déterministe : si on refait deux fois exactement la même expérience (en principe), on retrouve deux fois le même résultat. Et si on connaît l’état d’un système à un instant donné, on peut (toujours en principe) prédire ce que sera le résultat d’une mesure. En mécanique quantique, tout cela est parti en fumée : il existe un indéterminisme fondamental qui fait que les résultats des mesures dépendent du hasard, d’une manière qu’il est impossible de prévoir.

Cette idée a tellement choqué Albert Einstein que c’est à son sujet qu’il a déclaré son fameux « Dieu ne joue pas aux dés ». Il refusait de penser que le hasard pouvait jouer un rôle fondamental en physique. Et pourtant il avait tort.

3. La dualité onde-corpuscule

Je vous l’ai dit, en mécanique quantique on peut superposer les états. En particulier un objet microscopique peut se trouver dans plusieurs endroits à la fois : il suffit de superposer des états différents. On peut même pousser le bouchon plus loin et imaginer une particule qui soit dans une infinité d’endroits à la fois. Pour écrire ça, il faut superposer un nombre infini d’états différents. C’est un cocktail avec un nombre infini d’ingrédients !

Mais histoire que notre particule soit quand même un peu plus dans certains endroits que dans d’autres, on va mettre un coefficient à chacun des états qu’on superpose. Je vous ai dit que le coefficient que l’on met devant chaque état est relié à la probabilité de trouver notre particule dans cet état. Donc mathématiquement, on va définir une fonction P(x,y,z) qui va nous dire quelle est la probabilité de trouver notre particule dans chacun des points (x,y,z) de l’espace.

Vous voyez qu’en faisant cela, notre particule n’est plus un corpuscule localisé, mais elle est décrite par cette fonction P(x,y,z) que l’on va appeler un champ de probabilités. Ce champ partage plusieurs similitudes avec le champ électrostatique. Par exemple quand le temps s’écoule, ce champ peut évoluer et se comporter d’une manière qui ressemble beaucoup aux ondes électromagnétiques.Finalement on ne va plus décrire notre particule comme un objet ponctuel, mais comme une onde !

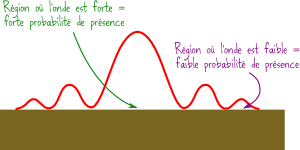
Cette description de la matière par des ondes avait été introduite au début du XXème siècle par plusieurs chercheurs, dont le physicien français Louis De Broglie. Ce dernier a notamment proposé l’idée de la dualité onde-corpuscule : les particules peuvent suivant les circonstances se comporter soit comme des particules, soit comme des ondes. Cette idée totalement contre-intuitive a permis de mettre un terme au débat multi-centenaire sur la nature de la lumière. Alors la lumière est-elle faite d’ondes électromagnétiques ou de photons ? Eh bien les deux mon général !

4. L’effet tunnel

Si vous m’avez suivi jusque là, vous avez compris qu’une des conséquences du principe de superposition, c’est qu’il faut admettre de décrire les particules par des ondes. Il y a plusieurs implications étranges de ce changement de perspective.
Revenons à notre ballon de foot : si vous le lancez contre un mur, il va rebondir. Il n’y a aucune chance qu’il traverse le mur comme par magie. Et pourtant avec les ondes c’est différent. Songez aux ondes sonores par exemple : si votre voisin d’à côté met la musique à fond, une partie du son va traverser et arriver chez vous. Certes le son sera atténué, voire très atténué, mais une petite partie passera quand même.

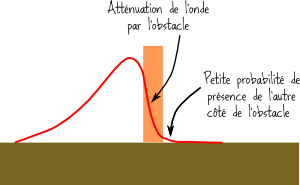
Maintenant imaginez un électron qui arrive sur un obstacle (une sorte de mur microscopique). Si cet électron est décrit par une onde, comme pour la musique de votre voisin, il y a une petite partie cette onde qui va passer de l’autre côté de l’obstacle (voir ci-contre).

Je vous rappelle que cette onde décrit une probabilité de trouver l’électron à un endroit donné. Donc ça veut dire qu’il y a une petite probabilité que l’électron traverse l’obstacle. On parle de l’effet tunnel, car tout se passe comme si une fois de temps en temps, un petit tunnel se créait dans le mur pour laisser passer notre électron.

L’effet tunnel est un autre exemple de ces choses qui se produisent dans le monde quantique, mais pas dans le monde macroscopique. Et il s’agit d’un phénomène avéré : on s’en sert pour faire des microscopes dits « à effet tunnel », qui permettent de voir et manipuler les atomes. L’effet tunnel permet également d’expliquer le principe de la radioactivité.

5. L’intégrale de chemin

Poursuivons notre exploration des conséquences innattendues de la description ondulatoire de la matière. Quand en physique classique les objets ont une position bien définie, ils suivent une trajectoire bien définie. Le coup-franc de Roberto Carlos passe à droite du mur, et pas à gauche.

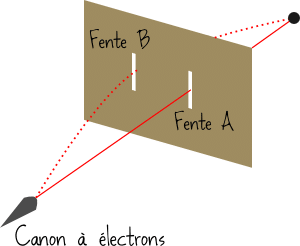
Mais en mécanique quantique, puisque les particules peuvent être à plusieurs endroits à la fois, elles peuvent aussisuivre plusieurs trajectoires à la fois ! L’illustration la plus spectaculaire de ce phénomène est celle de l’expérience de la double fente.

Dans cette expérience, on envoie des électrons sur un écran comportant seulement deux fentes par lesquelles ceux-ci peuvent passer. On peut montrer que même quand l’électron semble passer par la fente A, sa trajectoire dépend du fait que la fente B soit ouverte ou fermée.

On interprète cela en disant que même si l’électron passe principalement par A, un tout petit peu de lui essaye aussi de passer par B, et est donc sensible au fait que B soit ouverte ou fermée. (C’est comme si la trajectoire du coup-franc de Roberto Carlos était affectée par le fait de mettre un défenseur supplémentaire à gauche du mur !)

Le physicien Feynman (que je citais au début du billet) a poussé cette idée à son paroxysme, en écrivant que lorsqu’une particule quantique va d’un point à un autre, elle passe par tous les chemins possibles qui relient ces deux points. Une approche connue sous le terme d’intégrale de chemin.

6. La quantification

Nous y voici : je vais enfin vous parler de ce phénomène qui donne son nom à la mécanique quantique. Ca n’est pas forcément le plus spectaculaire, mais il a revêtu une importance historique fondamentale.

Comme d’habitude, voyons comment sont les choses en mécanique normale. Pour les objets macroscopiques, on utilise des quantités comme la position, la vitesse, l’énergie ou la vitesse de rotation. Ces quantités peuvent en principe prendre n’importe quelle valeur parmi les nombres réels. Ce sont des quantités continues.

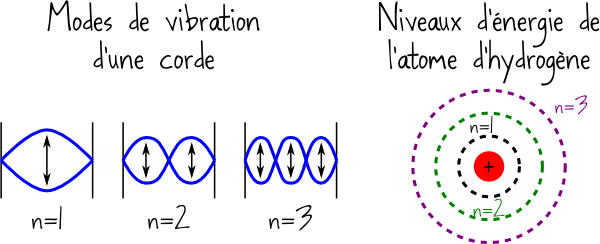
Mais en mécanique quantique, ça n’est plus nécessairement le cas ! Certaines quantités se trouvent contraintes à prendre des valeurs bien définies, on dit qu’elle sont quantifiées. Par exemple un atome d’hydrogène dans son état d’énergie minimale aura une énergie de -13.6 eV (eV, c’est l’électron-volt, l’unité d’énergie qu’on utilise pour les particules). Si on veut augmenter son énergie, alors on doit l’augmenter jusqu’à -3.4 eV. Impossible de lui donner une énergie intermédiaire entre ces deux valeurs ! Quant à diminuer son énergie, n’y pensez même pas, impossible de descendre sous la valeur de -13.6 eV ! Et c’est d’ailleurs heureux, car s’il n’y avait pas ça, les électrons iraient se crasher sur les protons, et les atomes seraient instables. La mécanique quantique a permis de résoudre ce paradoxe que la mécanique classique n’expliquait pas.

Mais au fait, pourquoi certaines propriétés seraient-elles quantifiées ? Encore une fois il est possible de la comprendre en considérant simplement la description ondulatoire des particules. Pensez à une autre onde : celle qui agite une corde de guitare. Puisque la corde est attachée aux deux extrémités, elle ne peut vibrer qu’à certaines fréquences. Les sons émis par une corde le sont donc à des fréquentes discontinues, et ne prennent pas des valeurs intermédiaires ! Il se passe le même phénomène pour les ondes qui décrivent les particules, et plusieurs quantités physiques qui décrivent les objets microscopiques sont quantifiées.

7. Le principe d’incertitude de Heisenberg

Pour ceux qui ont tenu jusque là, passons à la 7ème et dernière étape de ce voyage dans les mystères de la mécanique quantique. Le principe d’incertitude de Heisenberg est une des propriétés les plus caractéristiques mais aussi les plus étranges du monde quantique.

Quand je vous ai décrit l’idée de superposition des états, j’ai sous-entendu que l’on pouvait superposer tout et n’importe quoi. En fait ça n’est pas vrai ! Il y a des contraintes. La plus connue est qu’on ne peut pas spécifier à la fois exactement la position et la vitesse d’une particule. Plus sa position est précisément définie, plus sa vitesse est incertaine, et réciproquement. C’est le principe d’incertitude de Heisenberg.
Si vous êtes un peu familiers avec certains aspects des ondes acoustiques ou lumineuses, on peut illustrer ce principe. Quand on analyse un son, on peut regarder sa courbe en intensité, comme ce qu’on voit sur les logiciels d’enregistrement (ci-contre en bleu). Mais on peut aussi décomposer le son sur les différentes fréquences qui le composent (mathématiquement on utilise cette opération qui s’appelle la transformée de Fourier). On obtient alors un spectre de fréquences, c’est la courbe violette ci-contre.

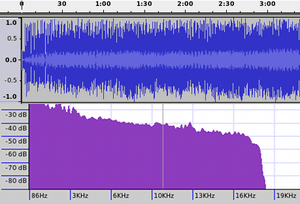
Or il s’avère que plus le son est court (comme un coup sec sur une batterie), plus il contient un nombre important de fréquences. Et réciproquement plus le son est pur en fréquence, plus il doit être long dans le temps.

Dans le son il y a donc une sorte de phénomène d’incertitude : il ne peut pas être à la fois localisé dans le temps (très court) et en fréquence (très pur). La situation est analogue pour la lumière : si vous voulez faire une onde à une longueur d’onde parfaitement définie, cette onde doit s’étendre partout dans l’espace ! Si vous voulez la localiser, il faut ajouter des fréquences supplémentaires.

En mécanique quantique, il se passe exactement la même chose. A partir du moment où on admet de décrire les particules par des ondes, alors il faut renoncer à pouvoir spécifier à la fois leur position et leur vitesse.

Pour résumer, comme le disait Heisenberg

« Chérie, j’ai garé la voiture, mais je sais plus où ».

Je m’arrête ici, j’ai clairement explosé mon record de longueur. Chacun de ces paragraphes mériterait un billet à lui seul. Ça viendra !

Pour aller plus loin…

Cette fois-ci, pas de « pour aller plus loin » en tant que tel. J’ai fait évidemment plein d’approximations, d’imprécisions et de simplifications dans ce texte. Si vraiment vous voulez aller plus loin, il faut s’attaquer à un cours de mécanique quantique ! Pour ma part, je recommande le livre « Modern Quantum Mechanics » de J.J. Sakurai, que j’avais trouvé très bien fait à l’époque (mieux que les classiques de Messiah ou Cohen-Tannoudji).

Quelques points au passage pour stimuler la réflexion de ceux qui connaissent déjà le sujet :

• Quand je parle de la superposition des états, je fais deux simplifications. J’ai écris qu’une particule peut être dans deux états à la fois. En fait elle est toujours dans un seul état (au sens « élément de l’espace de Hilbert »), mais cet état peut se décomposer sur deux états propres d’une observable d’intérêt (position, vitesse…). Autre simplification, quand j’écris des choses comme Chat = Mort Vivant, je suppose que l’on peut complètement décrire l’état à l’aide des valeurs propres d’une observable, ce qui n’est évidemment pas le cas. Il faudrait spécifier tout ça.
• Sur la mesure, un paradoxe qui me fascine : en principe la mécanique quantique doit être plus fondamentale que la mécanique classique. On doit donc pouvoir retrouver la mécanique classique comme une limite (du genre ) de la méca quantique. Or telle qu’elle est présentée ici, la mécanique quantique a fondamentalement  besoin de la mécanique classique pour définir les notions de mesure, réduction du paquet d’onde, etc. Pour surmonter cette difficulté, il faut creuser le concept de décohérence, mais je ne crois pas que ce paradoxe soit résolu.
• Sur le caractère fondamentalement probabiliste de la mécanique quantique, ma description laisse penser qu’il est possible que le hasard soit simplement le fruit de notre ignorance d’une connaissance suffisamment fine du système, un peu comme en physique statistique. Or il n’en est rien. La violation des inégalités de Bell par l’expérience d’Alain Aspect exclu de s’en sortir en supposant qu’il y a des variables cachées. Il faudra que je fasse un billet spécifique là dessus !
• Dans la dualité onde-corpuscule, je fais une analogie entre les ondes électromagnétiques et les ondes de probabilité. Attention cependant, contrairement aux apparences, le champ électromagnétique n’est pas la fonction d’onde du photon !
• Un point plus général : tous les effets que je décris ici sont censés exister pour les objets microscopiques mais pas pour les objets macroscopique. Où se situe la distinction ? Eh bien si vous avez un objet, vous pouvez calculer son action. Si cette action est grande devant la constante de Planck, les effets quantiques seront négligeables !

Source de l’article original :sciencetonnante.wordpress.com